(October 2012, Reddit-ed)
Solving the "Unblock Me" puzzle
| For the TL;DR crowd: I liked playing the Unblock-Me puzzle, so I coded an automatic solver, that works on screenshots taken from my phone. The code is on GitHub, and here is a video of the results. |
Even since I can remember, I've always been fascinated with puzzles. This fascination has manifested itself in temporary obsessions of various natures - mathematical, probabilistic, chess related, AI ... you name it, I've probably wasted time playing with it :‑)
A natural consequence is the kind of computer games I am drawn to... that is, puzzle games. I still consider Sokoban the best puzzle game I've ever played (and finished) - but also love most of Simon Tatham's collection. And recently, I started passing my half-hour train commutes to and from work, playing Unblock-Me on my iPhone.
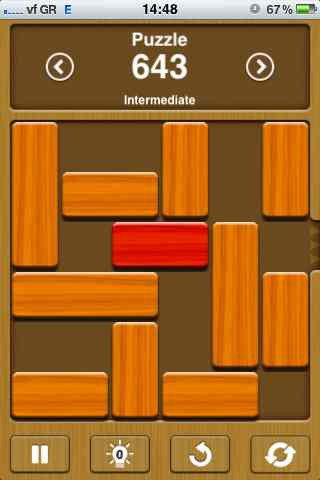
Would you like to play a game?
This game is deceptively simple: you have to move horizontal blocks left or right, and vertical blocks up or down, in order to free ("unblock") the red block - i.e. allow it to escape from the exit to its right. The red block is always at the 3rd line, as is the exit.
If you haven't played before, here's a link to a random Youtube video I found with a quick search. Apparently I am not the only one who likes this puzzle; there are lots of similar videos, with players showcasing how they solved a level they had trouble with. Obligatory warning: this game is very addictive, if you try it, there's no turning back.
My brain has more or less adapted, and quickly solves most of the levels. But now that I am close to completing the Expert set, there are some levels that torture me for minutes!
How dare they! :‑)
Time to use my brain - in a different way.
Stage 1: Detecting board sets from screenshots
On my iPhone, hitting both the main and the power button at the same time, results in an auto-saved 480x320 snapshot of the current screen (btw, that's how the picture you see above was obtained). Since the dimensions of this screenshot are constant, the placement of the tile grid will also remain constant: at identical pixel positions in every such snapshot.
(Translation: if you want to replicate my results in phones with different screenshot sizes... you'll have to edit my code :‑)
This means we can do a small number of tests, and identify the tile coordinates in these snapshots:
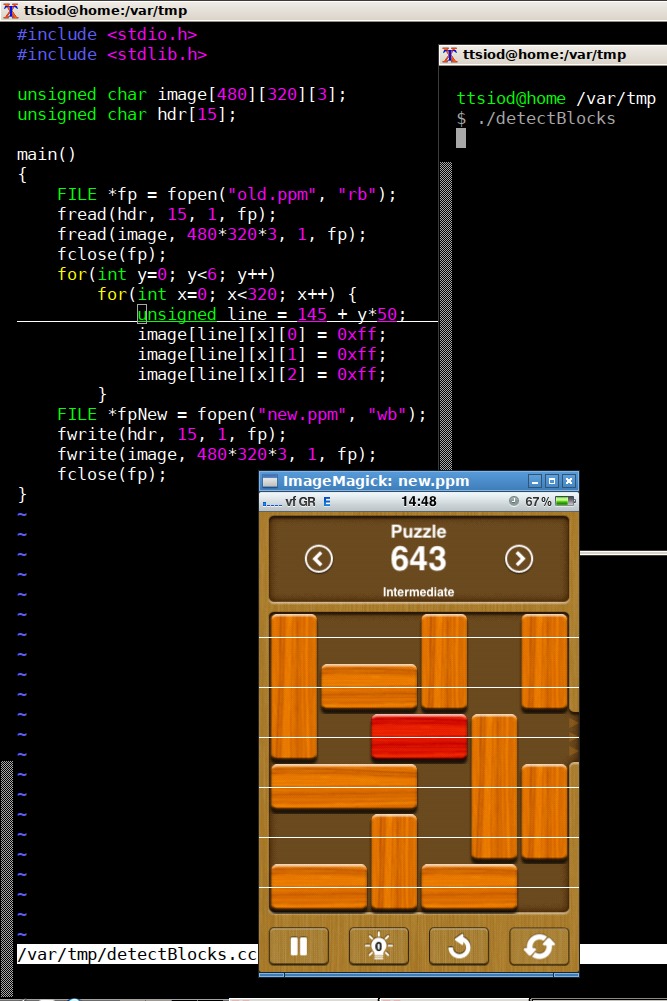
Hunting down the tile coordinates
In the screenshot above, you see how I manipulated the .ppm data of the image (generated via ImageMagick: "convert IMG_0354.PNG old.ppm") and emitted horizontal lines. Fine-tuning the location of these white lines allowed me to find where the tile centers are located, in both horizontal, and (via a similar pass) vertical coordinates.
At that point ...
- I sampled the color of the center pixel of each tile - and mapped the RGB values into the 3 tile categories (empty, block and prisoner) via threshold values that I experimented with.
- I sampled the top center and the bottom center pixel of each tile - and stored whether it's RGB values thresholded as white, black, or non-border. The game uses these colors to "shade" the blocks, and thus allowed me to learn the vertical "borders" between blocks.
I could then write a simple algorithm that re-created the block information from these two arrays:
// The board is SIZE x SIZE tiles #define SIZE 6 // The tile "bodies" information - filled by DetectTileBodies() // via heuristics on the center pixel of the tile // enum TileKind { empty = 0, block = 1, prisoner = 2 }; static TileKind g_tiles[SIZE][SIZE]; // The top and bottom "borders" of each tile // (hence the 2x in the vertical direction) // filled by DetectTopAndBottomTileBorders() // enum BorderKind { notBorder = 0, white = 1, black = 2 }; static BorderKind g_borders[2*SIZE][SIZE]; // The board is a list of Blocks: struct Block { static int BlockId; // class-global counter, used to... int _id; // ...uniquely identify each block int _y, _x; // block's top-left tile coordinates bool _isHorizontal; // whether the block is Horiz/Vert TileKind _kind; // can only be block or prisoner int _length; // how many tiles long this block is Block(int y, int x, bool isHorizontal, TileKind kind, int length): _id(BlockId++), _y(y), _x(x), _isHorizontal(isHorizontal), _kind(kind), _length(length) {} }; int Block::BlockId = 0; // This function (called at startup) scans the g_tiles and g_borders // arrays, and understands where the blocks are. // // Returns a list of the detected Blocks list<Block> ScanBodiesAndBordersAndEmitStartingBlockPositions() { list<Block> blocks; bool isTileKnown[SIZE][SIZE]; // Initially, we don't have a clue what each tile has memset(isTileKnown, false, sizeof(isTileKnown)); while (true) { for(int y=0; y<SIZE; y++) { for(int x=0; x<SIZE; x++) { if (isTileKnown[y][x]) // Skip over tiles we already know continue; if (empty == g_tiles[y][x]) { // Skip over empty tiles isTileKnown[y][x] = true; continue; } bool isMarker = (g_tiles[y][x]==prisoner); const char *marker = isMarker?" (marker)":""; // Use the border information: if (g_borders[2*y][x] == white && g_borders[2*y+1][x] == black) { // If a tile has white on top and black on bottom, // then it is part of a horizontal block isTileKnown[y][x] = true; int xend = x+1; // Scan horizontally to find its end while(xend<SIZE && g_borders[2*y+1][xend] == black && g_borders[2*y][xend] == white) { isTileKnown[y][xend] = true; xend++; } // two adjacent blocks of length 2 would lead // to a 'block' of length 4... if (xend-x==4) { // ...in that case, emit two blocks of length 2 cout << "Horizontal blocks at " << y << "," << x; cout << " of length 2 " << marker << "\n"; blocks.push_back( Block(y,x, true, g_tiles[y][x], 2)); blocks.push_back( Block(y,x+2, true, g_tiles[y][x+2], 2)); } else { // ... otherwise emit only one block cout << "Horizontal block at " << y << "," << x; cout << " of length " << xend-x << marker << "\n"; blocks.push_back( Block(y,x, true, g_tiles[y][x], xend-x)); } } else if (g_borders[2*y][x] == white) { // If a tile has white on top, but no black // on bottom, then it is part of a vertical block. isTileKnown[y][x] = true; int yend = y+1; // Scan vertically to find its end while(yend<SIZE && g_borders[2*yend+1][x] != black) { isTileKnown[yend][x] = true; yend++; } cout << "Vertical block at " << y << "," << x; cout << " of length " << yend-y+1 << marker << "\n"; blocks.push_back( Block(y,x, false, g_tiles[y][x], yend-y+1)); } else // either an empty, or a body-of-block tile isTileKnown[y][x] = true; } } bool allDone = true; for(int y=0; y<SIZE; y++) for(int x=0; x<SIZE; x++) allDone = allDone && isTileKnown[y][x]; if (allDone) break; } return blocks; }
With the exception of neighbouring horizontal blocks - which I had to hack around - it worked on the first try. Feeding it with screenshots, I saw it emit the board information:
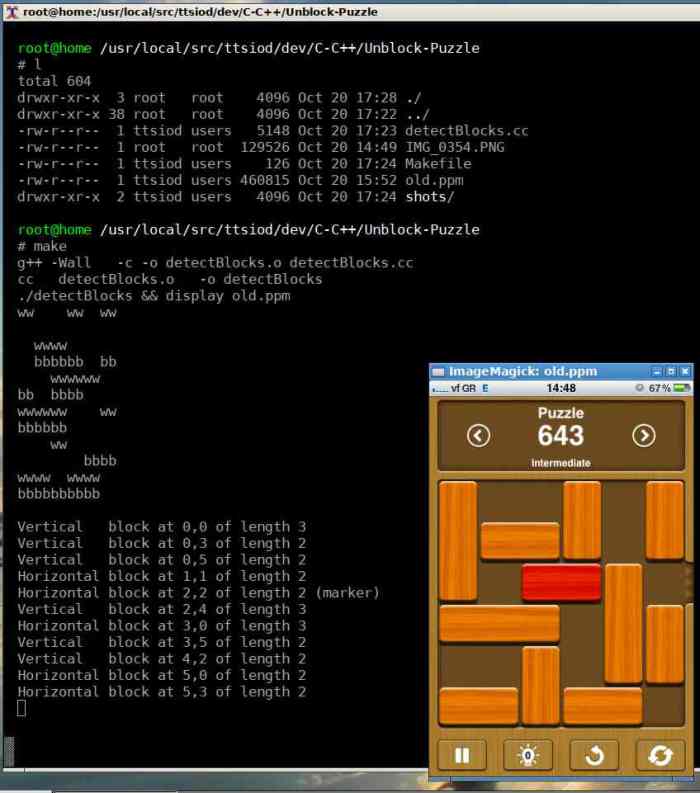
From screenshot to block data
Stage 2: The Solver
So, I had a list of blocks that represented a board - what then?
Well, from each such list, I could generate ... a list of such lists - that is, the list of possible boards that can be reached from this one, by moving a block one position to the left, right, top or bottom.
Following the same approach I used in my Knight's Tour, I wrote a brute-force recursive traversal:
void SolveBoard( board ) { can prisoner escape? he can! Bliss he cant? for each possible board that can arise out of the current one SolveBoard(newBoard) }
I also added a set<Board> that was checked upon SolveBoard entry, so that the algorithm never went back to a position that it had already passed through before (in the call stack).
And run it...
And waited...
Did some web browsing. Went for some coffee...
Came back - still running.
Apparently, the problem space of this puzzle is not as small as I thought - this recursive attempt at finding the solution, goes "deep" first, exhausts the "move" it tried, then tries another.
In computer-science parlance, what I did was a "depth-first" search of the solution - meaning that the algorithm descended the tree of possible moves all the way to it's leaves (i.e. to the board states where there is no move left), and then backtracked back to try something else. And as is obvious on hindsight, this will only work for "small" problem spaces - like my Knight's Tour search. In UnblockMe however, the combinations of moves one can do at every level, multiply with the ones he can do on the next one - and basically, "explode" exponentially.
Instead of diving "deep" in the tree, I had to visit it in "layers" of increasing depth - i.e. in Breadth First Search:
Enqueue the current board while Q not empty: Dequeue a board and examine it can prisoner escape? he can! Bliss he cant? for each possible board that can arise out of this one add board to END of Q
The pseudocode above visits the first level of available moves, then all the second-level moves, then the 3rd, etc. This means that it finds the optimal solution - the one the prisoner can use to escape, in the least amount of moves.
The actual implementation, below, has to account for not visiting already visited boards, and for tracing back from the solved board into the one we started from - I used a map<Board,MoveIusedToGetThere> to do that.
// When we find the solution, we also need to backtrack // to display the moves we used to get there... // // "Move" stores what block moved and to what direction struct Move { int _blockId; enum Direction {left, right, up, down} _move; Move(int blockID, Direction d): _blockId(blockID), _move(d) {} }; ... // The brains of the operation - basically a Breadth-First-Search // of the problem space: // https://en.wikipedia.org/wiki/Breadth-first_search // void SolveBoard(list<Block>& blocks) { cout << "\nSearching for a solution...\n"; // We need to store the last move that got us to a specific // board state - that way we can backtrack from a final board // state to the list of moves we used to achieve it. map< Board, Move> previousMoves; // Start by storing a "sentinel" value, for the initial board // state - we used no Move to achieve it, so store a block id // of -1 to mark it: previousMoves.insert( pair<Board,Move>(renderBlocks(blocks), Move(-1, Move::left))); // We must not revisit board states we have already examined, // so we need a 'visited' set: set<Board> visited; // Now, to implement Breadth First Search, all we need is a Queue // storing the states we need to investigate - so it needs to // be a list of board states... i.e. a list of list of Blocks! list< list<Block> > queue; // Start with our initial board state queue.push_back(blocks); while(!queue.empty()) { // Extract first element of the queue list<Block> blocks = *queue.begin(); queue.pop_front(); // Create a Board for fast 2D access to tile state Board board = renderBlocks(blocks); // Have we seen this board before? if (visited.find(board) != visited.end()) // Yep - skip it continue; // No, we haven't - store it so we avoid re-doing // the following work again in the future... visited.insert(board); // Check if this board state is a winning state: // Find prisoner block... list<Block>::iterator it=blocks.begin(); for(; it!=blocks.end(); it++) { Block& block = *it; if (block._kind == prisoner) break; } assert(it != blocks.end()); // The prisoner is always there! // Can he escape? Check to his right! bool allClear = true; for (int x=it->_x+it->_length; x<SIZE ; x++) { allClear = allClear && !board(it->_y, x); if (!allClear) break; } if (allClear) { // Yes, he can escape - we did it! cout << "Solved!\n"; // To print the Moves we used in normal order, we will // backtrack through the board states to print // the Move we used at each one... list<list<Block> > solution; solution.push_front(copyBlocks(blocks)); map<Board,Move>::iterator itMove = previousMoves.find(board); while (itMove != previousMoves.end()) { if (itMove->second._blockId == -1) // Sentinel - reached starting board break; // Find the block we moved, and move it // (in reverse direction - we are going back) for(it=blocks.begin(); it!=blocks.end(); it++) { if (it->_id == itMove->second._blockId) { switch(itMove->second._move) { case Move::left: it->_x++; break; case Move::right: it->_x--; break; case Move::up: it->_y++; break; case Move::down: it->_y--; break; } break; } } assert(it != blocks.end()); // Add this board to the front of the list... solution.push_front(copyBlocks(blocks)); board = renderBlocks(blocks); itMove = previousMoves.find(board); } // Now that we have the full list, emit it in order for(list<list<Block> >::iterator itState=solution.begin(); itState != solution.end(); itState++) { printBoard(*itState); cout << "Press ENTER for next move\n"; cin.get(); } cout << "Run free, prisoner, run! :-)\n"; exit(0); } // Nope, the prisoner is still trapped. // // Add all potential states arrising from immediate // possible moves to the end of the queue. for(it=blocks.begin(); it!=blocks.end(); it++) { Block& block = *it; #define COMMON_BODY(direction) \ list<Block> copied = copyBlocks(blocks); \ /* Add to the end of the queue for further study :-) */ \ queue.push_back(copied); \ /* Store board and move, so we can backtrack later */ \ previousMoves.insert( \ pair<Board,Move>( \ renderBlocks(copied), \ Move(block._id, Move::direction))); if (block._isHorizontal) { // Can the block move to the left? if (block._x>0 && empty==board(block._y, block._x-1)) { block._x--; COMMON_BODY(left) block._x++; } // Can the block move to the right? if (block._x+block._length<SIZE && empty==board(block._y, block._x+block._length)) { block._x++; COMMON_BODY(right) block._x--; } } else { // Can the block move up? if (block._y>0 && empty==board(block._y-1, block._x)) { block._y--; COMMON_BODY(up) block._y++; } // Can the block move down? if (block._y+block._length<SIZE && empty==board(block._y + block._length, block._x)) { block._y++; COMMON_BODY(down) block._y--; } } } // and go recheck the queue, from the top! } }
And to my immense delight, I saw it work:
No, this is not cheating! It's a product of my own brain, addressing the same problem... in a different way. It just so happens... that I know how to extend my brain :‑)
Some thoughts
The code lives in GitHub, and it's relatively simple to follow through (I commented it a lot). However, if you compare this implementation with the one I did for Score4, you will naturally notice the verbosity of C++. Why didn't I use OCaml for this? Or even C++11, which would drastically cut down on e.g. iterator loops?
Well - the problem parameters... are that I want to run this on my phone. And as it turns out, I have succeeded in installing a Linux-based cross compiler for my jailbroken iPhone - but it only works for old-style C++ (i.e. non-C++11).
OCaml on the iPhone would be cool, though - if I ever get my hands on an iPhone OCaml compiler, I'll probably port my code.
Update, Oct 22, 2012: I did a quick "port" to C++11.
Update, Oct 27, 2012: I ported the code to OCaml.
| Index | CV | Updated: Tue Jun 13 20:40:05 2023 |


